Investor pasti fokus pada kemungkinan keuntungan dengan tinggi. Namun, investor juga perlu mempertimbangkan besarnya volatilitas saham dan risiko yang harus ditanggung sebagai imbas dari potensi keuntungan investasi yang tinggi. Kendati kita sering membahas tentang risiko dalam pengertian umum, ada pula teori formal akan eratnya kaitan antara risiko dan keuntungan.
Misalnya, rasio Sharpe mengukur kelebihan keuntungan per unit risiko, di mana risiko dihitung sebagai volatilitas, yang merupakan ukuran risiko tradisional dan populer. Properti statistiknya terkenal dan digunakan dalam beberapa kerangka kerja, seperti teori portofolio modern dan model Black-Scholes.
Dalam artikel ini, kita akan membahas volatilitas saham untuk memahami kegunaannya dan batasannya.
Pengertian Volatilitas Saham
Volatilitas saham adalah deviasi standar keuntungan tahunan yang ditunjukkan dari naik turunnya harga saham. Dalam kerangka teori tradisional, volatilitas tidak hanya mengukur risiko, tetapi memengaruhi ekspektasi keuntungan jangka panjang di periode selanjutnya.
Volatilitas tinggi adalah pedang bermata dua: mengikis keuntungan jangka panjang yang mungkin Anda dapatkan, tetapi juga memberi Anda lebih banyak peluang untuk menghasilkan keuntungan besar.
Deviasi Standar Tahunan
Tidak seperti volatilitas tersirat yang digunakan dalam teori penetapan harga opsi dan merupakan perkiraan berwawasan ke depan berdasarkan konsensus pasar, volatilitas reguler terkesan melihat ke belakang. Tepatnya, volatilitas reguler adalah deviasi standar tahunan dari keuntungan historis.
Kerangka risiko tradisional yang mengandalkan standar deviasi umumnya mengasumsikan keuntungan mengikuti distribusi normal berbentuk lonceng. Pada distribusi normal, sekitar dua pertiga (68,3%) berada dalam rentang satu SD (+/-); dan berada dalam dua deviasi standar sebesar 95%.
Dua penanda grafik distribusi normal adalah ekor tipis dan simetri sempurna. Ekor tipis menunjukkan tingkat kemungkinan lebih yang sangat rendah (sekitar 0,3%) dari tiga standar deviasi dari rata-rata. Simetri berarti frekuensi dan besar keuntungan naik setara dengan kerugian sisi bawah.
Akibatnya, metode tradisional menganggap semua ketidakpastian sebagai risiko, tidak peduli arahnya. Ini menjadi masalah jika keuntungan nilai investasi yang tidak simetris. Mereka khawatir tentang kerugian mereka “di sebelah kiri” dari rata-rata, tetapi mereka tidak khawatir tentang keuntungan “di sebelah kanan” rata-rata.
Mari menggunakan dua saham fiksi untuk menggambarkan kejanggalan ini. Stok yang menurun (garis biru) sama sekali tanpa dispersi, sehingga menghasilkan volatilitas nol. Namun saham yang naik — karena menunjukkan beberapa guncangan naik, tanpa ada satu penurunan sekalipun — menghasilkan volatilitas (deviasi standar) 10%.
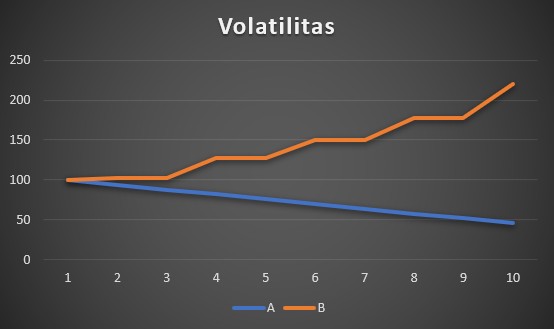
Penjelasan Teori dan Rumus
Rumus volatilitas adalah Volatilitas = σ√T.
Contohnya, volatilitas untuk indeks S&P 500 per Maret 2021, kami mendapatkan kisaran dari 13,48%. Dan rangkaian keuntungan yang kami dapatkan bisa diperpanjang kembali selama periode historis dengan durasi berapa pun, seperti tiga tahun, lima tahun, atau 10 tahun.
Volatilitas meningkat seiring dengan peningkatan interval, tetapi tidak terlalu proporsional: dalam seminggu bukan sejumlah lima kali lipat jumlah harian, dan dalam sebulan bukan sejumlah empat kali lipat mingguan. Kita telah sampai pada aspek kunci teori random walk: skala deviasi standar (peningkatan) sebanding dengan akar kuadrat waktu.
Oleh karena itu, jika deviasi standar harian adalah 1,2%, dan jika ada 253 hari perdagangan dalam setahun, standar deviasi tahunan adalah standar deviasi harian 1,2% dikalikan dengan akar kuadrat dari 250 (1,2% x 15,9 = 1,908%) . Dengan rumus ini, kita dapat menganualisasikan standar deviasi interval untuk sebuah indeks dengan mengalikan dengan akar kuadrat dari jumlah interval dalam satu tahun.
Sifat teoritis lain dari volatilitas adalah kemungkinannya dalam mengurangi keuntungan nilai investasi. Entah Anda terkejut atau tidak dengan fakta ini, kenyataannya hal ini disebabkan asumsi utama dari ide random walk: keuntungan investasi ditunjukkan dalam bentuk persentase.
Semisal Anda mulai investasi Rp1.000.000 dan kemudian mendapatkan 10% untuk mendapatkan Rp1.100.000. Kemudian Anda kehilangan 10% di mana Anda hanya mendapatkan Rp990.000 (Rp1.100.000 x 90% = Rp990.000).
Lalu, Anda mendapatkan 10% lagi, menjadi Rp1.089.000 (Rp990.000 x 110% = Rp1.089.000). Pada akhirnya, Anda mendapat nilai bersih Rp980.100 setelah kehilangan 10%. Hal seperti ini memang kontra-intuitif, tetapi modal Anda perlahan-lahan terkikis, meskipun keuntungan rata-rata Anda 0%!
Apabila Anda mengharapkan keuntungan tahunan rata-rata 10% per tahun dengan rata-rata aritmetika, ternyata keuntungan jangka panjang yang Anda dapatkan kurang dari 10% per tahun. Faktanya, jumlah tersebut berkurang sekitar setengah variance (standar deviasi kuadrat). Dalam hipotesis murni di bawah ini, kita akan mencoba investasi awal Rp1.000.000 dengan volatilitas selama lima tahun, yang berakhir dengan nilai Rp1.570.000:
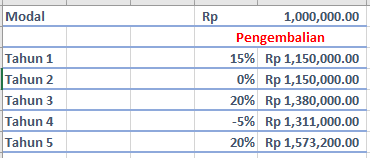
Keuntungan tahunan rata-rata selama lima tahun adalah 10% (15% + 0% + 20% – 5% + 20% = 50% ÷ 5 = 10%), tetapi tingkat pertumbuhan tahunan gabungan (CAGR, atau keuntungan geometris) yang menjadi ukuran yang lebih akurat dari realisasi keuntungan hanya 9,49%.
Volatilitas mengikis hasilnya, dan perbedaannya sekitar setengah dari varian 1,1%. Hasil ini bukan dari contoh historis, tetapi dalam hal ekspektasi, diberikan:
σ = deviasi standar
σ2 = sebagai varians yang merupakan kuadrat dari deviasi standar
μ = sebagai rata-rata perolehan yang diharapkan
Sehingga rumus keuntungan rata-rata tahunan yang diharapkan:
μ− (σ2 ÷ 2)
Sumber: Investopedia.

